面对这样细节严重丢失的图片,我们该怎样进行修复呢?

下面是我们修复的效果:

那么,我们该如何调整,才能达到这种效果呢?
这里就涉及到一个非常重要的术语:伽马值。
在摄影中,我们会经常遇到一组相近的概念:曝光和伽马值。

我们先看一张图片:

如果我们降低曝光值:

画面的变化是:

如果我们降低伽马值:
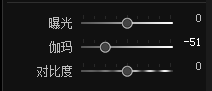
画面的效果是:

很明显,你可以发现二者的区别。
我们再看一张图:

如果我们提高曝光值:

画面效果是这样的:

如果我们提高伽玛值:

得到的画面效果是:

你也可以很明显的发现二者的不同。
那么,这二者的区别到底在哪里呢?
我们先从伽玛值讲起(下面这一段很无聊,不想了解的可以略过):
一开始,伽玛值是一个专有名词,后来被广泛运用于图像灰度映射的校正。宏观上我们看到的就是,Gamma变了,图像亮度就跟着变了,本质上是信息的映射关系在数学上变了。以下是正文:
Gamma是在计算机图形领域最不容易被理解掌握的概念之一,其中有很大一部分原因要怪它到处出现,极容易让人混淆。Gamma的最初定义如下:“Gamma是用来描述显示设备的‘非线性’程度的专有名词”。这是历史上Gamma所拥有的第一个定义。但是很显然这样的一个定义并不能解释清楚任何的问题。
那么要解释清楚Gamma,首先要解释的就是显示设备的“非线性”。
一切的显示设备,比如计算机的显示屏幕、手机或平板电脑的屏幕、老式的阴极摄像管电视机(CRT电视机),或是新式的液晶屏幕电视机,都是“非线性的”。以最为典型的CRT(Cathode ray tube阴极射线管)显示屏幕为例(无论是电脑或者电视机),所谓“非线性”即意味着,如果施加在阴极摄像管的电压强度 V 增加1倍,屏幕表面所输出的光强度 I 并不会很理想的相应增加一倍。
反过来说,如果显示器所用到的发光元件是一个理想的物理模型,在输入电信号强度V(Voltage,电压)和输出的光照强度I(Intensity,强度)转化过程中,V与I的比值是一个常数k,这里我们就可以说这个发光元件是一个线性元件,转化是线性转化,是对电信号的“无损转化”。
表达通俗一点,以上公式表示这样一个意思:在理想的线性的显示元件中,一份电压强度可以生成一份相对应的光照强度,电压翻几倍,光照强度也会相应跟着翻几倍。
当然现实世界中的任何显示器都不会有这样理想的特性,幸运的是,这些有损的显示元件的输入电压V 与输出光照强度 I的对应关系在数学上呈现简单的规律,可以看到非线性显示元件的输入-输出公式与线性显示元件的公式非常相近,唯一的不同就是在输入信号V的右上角多了一个指数γ,这个希腊字母γ读作Gamma(中文音“伽马”),它便是用来描述非线性元件输入信号 V 在转化成光线强度 I 过程中“非线性”程度的唯一一个参数。
表达通俗一点就是说,非线性显示元件呈现这样的规律:输入电信号V的大小在乘方Gamma和乘以常数k之后,会得到相对应的输出信号 I,无论输入电压的大小与否,一个非线性元件的信号损耗特性Gamma是固定的。
然而不同的显示设备,Gamma的大小是不尽相同的,常见的Gamma大小可能会在1.4到2.6之间,苹果电脑显示器的Gamma在1,8左右,传统CRT电视机的Gamma在2.35-2.55之间。总结来说,Gamma是跟着硬件设备走的,和电压以及光强度没有关系。
那么到这里,我们就终于能理解为什么Gamma的定义是“用来描述显示设备非线性程度的专有名词”了,理想的显示元件,电信号以线性比例对应光强度,Gamma=1,而现实世界中非线性的显示元件,Gamma≠1,Gamma越大,信号损失越大,信号的“失真”程度越高,因此Gamma就可以用来表示一个显示元件对信号的失真程度。
这里必须要强调的是:“理想的,信号无损的显示元件”,并不是说在电压到光强度的转化过程中毫无能量损失,而是只要电压以k倍转化为相对应的光强度就可以,一份电压对应一份光强即可,等比例转化即可,即 y=kx 的线性映射,此时Gamma是等于1的。
而非线性显示元件在得到输出光强 I 之前,需要把输入电压 V 在k倍的基础上,右上角再次乘方一个Gamma,那么此时这个Gamma可以比1大,亦可以比1校
在计算机图形学中,输入的电压信号 V 和输出的亮度信号 I 都是在0-1(这个0就对应着电压为0,颜色为黑色,1就对应着电压为最大,光强度最高,颜色为白色)区间浮动的,如果这样描述问题的话,我们连公式中间的常数k都可以忽略不计了,输入-输出的公式就简化成了:

OK,上面这一大段话的核心意思是(这个总结可以看一下):
所谓伽马值,原本是用来描述硬件的失真程度,伽玛值越大,失真程度越大。
后来应用到计算机图像领域,便成为了一个用来校正画面明暗程度的数学工具。
_ueditor_page_break_tag_
回到前面的问题,我们打开图片:

然后调低伽马值。
我们还可以新建一个渐变滤镜,进一步调整上面的细节:
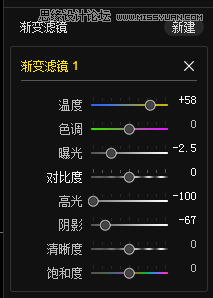

我们再调整一下曲线:
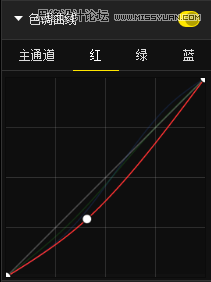
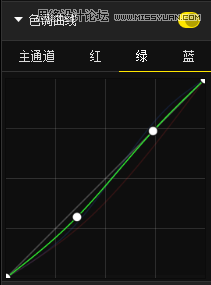
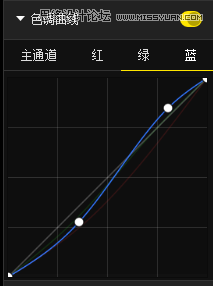
画面效果如图:

与原图对比:







