曲线的绘制如同打铁,达到恰到好处是一门手艺。以iOS 7电话图标为例,介绍一种用 Adobe Illustrator 绘制复杂光滑曲线的策略。
复杂光滑曲线不是指线条的宏观形状复杂,比如有很多凸起、凹陷、转折和突变之类,它从宏观上看就是一整条曲线,光滑指的是曲线过渡顺畅,无论是急速的还是柔和的过渡,都是光滑顺畅的。策略指的是一种制作的方法,它可能并不牵扯到基本原理层面,而曲线的原理层面就是数学,在这只是一种应用。
但也从一些制作的曲线基本概念开始。
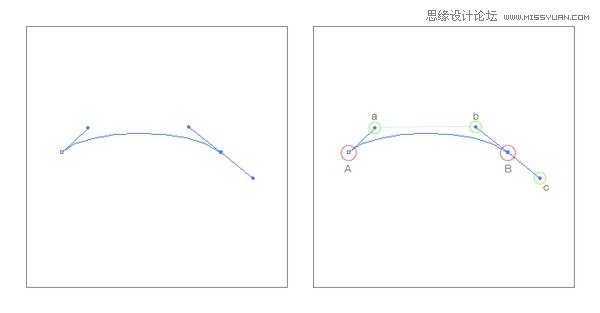
Adobe Illustrator 和其他平面矢量软件一样,使用的是贝塞尔曲线,而且是三次曲线,用四个控制点来描述和控制曲线,而在 Illustrator 中控制部分定为了锚点和手柄,所以一段曲线是由首尾两个锚点控制线条的始末位置,而首尾的手柄控制线条的形态。
在用钢笔工具来绘制曲线时,就是点击 A 拖动到 a 再点击 B 拖动到 c 也就是确定了 b 形成 AB 这条曲线,那么,在通常情况下使用钢笔来绘制曲线是通过拖动来实现的,而不像三维软件中的一些曲线绘制工具是通过放置 A a b B 来实现的,Illustrator 的这种绘制方法的好处就是感觉更易控制(感觉上是两个点来确定的),缺点最明显一点就是 c,也就是说当你要绘制 b 时,c 已经确定,也就是说这段曲线如果还要延续下去,那么 c 已经事先确定了,如果你在绘制 B 点时,对下一段的曲线没有概念的话,只为了达到 b 的要求放置了 c 而没有意识到下一段,将给绘制工作带来更多的后续工作,通过再调整手柄控制点。
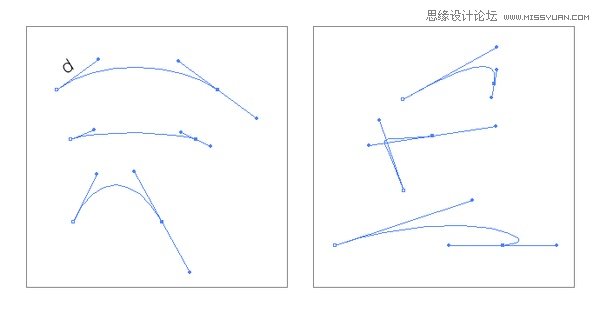
在一些介绍曲线绘制教程中,可以看到一个 1/3 规则,也就是从锚点到手柄控制点的距离 d 大概是 1/3 曲线长度,这当然是一种通常的经验,并不是要严格遵守的,需要看曲线的形态。
1/3 规则是为了避免类似右边出现的情况。其实这个规格很容易理解,我们追求的曲线在数学描述上应该越简单越好,简单不只是数量上最少,比如最少的控制点,还有一个重要点就是均匀,均匀就是每一个控制点的权重是均匀的,不一定每一个控制点的权重要一样,但是如果左右锚点间的曲线是对称的,那么控制点的权重就需要一样,不仅包括曲线拉伸的权重还包括曲线方向的权重。简单说就是不能过分拉伸以及松弛,而是以简单的方法保持紧绷。
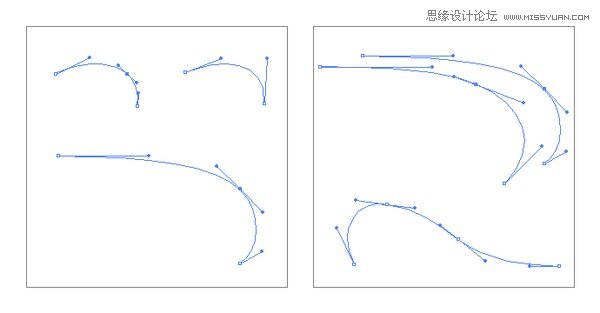
一段曲线,即两个锚点两个手柄形成的曲线是容易绘制和控制的,只需要耐心调整就可以了,因为任何变化都可以在容易控制的范围内。但是,复杂的曲线不是两个锚点形成的一段曲线,它至少得是三个锚点以上。
如果我们去绘制一段曲线,能使用两个锚点来形成当然是最好,如果此时在曲线中间再放置一个锚点是自添麻烦,一下子将军控制的复杂度翻倍,但是由于形状的需求,必须要放置更多的锚点,一段简单曲线能表达的形状是有限的。
多了一个锚点,去拟合一条曲线,所谓拟合就是比如先手绘好的形状然后扫描将图像输入软件然后是勾画轮廓,有时我们并没有这个步骤,比如对照着手绘直接绘制,而且单凭一个脑袋,有的甚至凭感觉,这时候,会出现一个情况,就是绘制一条看上去形状差不多的曲线,可以有很多绘制方法,锚点放这可以,放在那也可以,只不过把手柄拖长一点,那么该如何选择呢。
凭感觉,凭经验,因为这是手艺。不过,重要的是要记住”均匀”这个词,追求”最简单”。
一旦将锚点增加到 4 个呢,这将会变得非常非常复杂,即使有经验的人,依然需要通过后续不断的调整来取得满意结果。
绘制曲线的目标是确定,而不是看上去差不多就行了,也就是包含在”简单”之内,每一个点都能确定,就像一个圆形,它的几个控制点就是确定的。而我们绘制曲线的确定当然不是 100% 的确定,而且一种确切感,如果经验丰富,就能知道下一个控制点在什么位置了。
但是,如果一段曲线是对称的,那么我们就多了一种确定了, 在绘制锚点的时候就可以左边这一点与右边这一点同样高,依此类推,我们可以找到很多确定,或者去拟合这种确定,比如比例上的,这段是那段的一半等等。而是用网格辅助来作图,也可以视作是寻找确定。
即使我们使用了网格,确定了 4 个锚点的以及手柄拉伸的长度和方向,也需要很大的工作量,而在实际中我们使用的方法还是依赖于眼睛,达到大概需求后再去规整尺寸,锚固好这些”确定”,在规整过程中不断调整。
但这种方式是没有效率的,尤其是锚点数量达到和超过 4 个的复杂曲线的时候。

类似 iOS 7 电话图标的形状,左右对称显而易见,但是很难用 3 个锚点来确定这个形状,尤其是还要求”均匀”,没有过分拉伸或者形状拟合程度高。
用 Illustrator 来绘制曲线的时候,很少是直接下手绘制的,正是因为我们上面说的曲线没有确定性,不像四边形和圆形以及这些基本形状的组合图像那样,确定是事先的。所以无论我们是不是输入手绘进行拟合,在绘制过程中总是处在一种拟合状态的。
而在这提出的一中绘制策略,就是在这些复杂光滑曲线的绘制过程中引入更多的确定性,就像意识到图形是对称一样,我们要找到一些内在逻辑,控制着线条以可控的方式组合成。
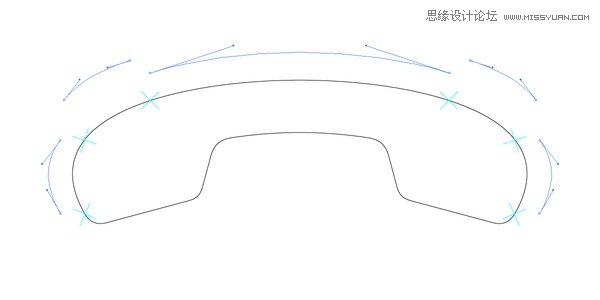
这种策略就是曲线的拆解,将复杂光滑的曲线拆解中曲线绘制最基本的单位,就是两个锚点两个手柄的一段曲线,然后就拆解后的曲线连接,再作一些细微调整。
两个锚点的曲线是可控的,也就是说有很高的确定性,而且手柄长度是独立控制的,而不像通常绘制中(见开头说的我们是通过绘制 c 来取得 b 的)前后影响的巨大,而手柄方向在绘制和后续连接和调整过程中很容易控制。
那么曲线绘制的技艺就转变为曲线拆解的技艺了,而拆解的技艺仍然以”均匀”和”简单”为宗旨,也就是说如果有对称和类似对称,那就是最容易拆解的部分了,如果很难拆解,那么我们去分析曲线的曲率变化,结合我们对两个锚点的基本曲线的可供形状的意识,以”简单”为目标去寻找却开点。
这种拆解策略在三维中也是通用的,只不过操作手段不一样而已,在这,我们依赖的操作手段就是开头的曲线的基本控制单元。
注:图形只是示例,这种拆解并不唯一,而且我是通过自己的方式去拟合 Apple 的那个 120*120 px 的图标,误差肯定很大。这种方法是在三维和二维之间互导发现的,比如将一条高阶的光滑曲线导入三次贝塞尔曲线环境中,看软件是如何自动放置锚点的。






